AVL Tree | Java Development Journal

In this article, we are going to cover the AVL tree and what makes them so special and so difficult to implement. We will also see the balance factor and rotations required to make this a balanced binary tree. Finally, we will code the AVL tree in Java.

1. What is AVL Tree?

AVL tree is named after its inventors, Adelson-Velsky and Landis. They invented the AVL tree in 1962. We can define the AVL tree as a balanced binary tree whose height is balanced. In the AVL tree, each node is associated with a balance factor and the tree is said to be balanced if the balance factor of each node of the AVL tree is between -1 to 1. If the balance factor is not in this range, then the tree is not balanced and it has to be balanced via rotations (later in this article).

So, as you might have guessed, the key property of the AVL tree is to stop a tree from becoming skewed. A skewed tree has worst-case time complexity for tree operations, i.e., O(n). Thus, by keeping the tree balanced, the AVL tree ensures that the worst-case time complexities for tree operations would be O(log n), where n is the number of nodes in the tree.

2. Balance Factor in AVL Tree

To calculate the balance factor of node N of the tree, we use the following formula:

Balance Factor (N) = height (left(N)) - height (right(N))

Balance factor of 1 means that the left sub-tree is higher than the right sub-tree by 1 level.
Balance factor of 0 means that the height of the left sub-tree and of the right sub-tree are equal.
Balance factor of -1 means that the right sub-tree is higher than the left sub-tree by 1 level.

Here is the Node object for our tree

public class AVLNode {

    AVLNode left, right;
    int data;
    int height;

    public AVLNode() {
        left = null;
        right = null;
        data = 0;
        height = 0;
    }

    public AVLNode(int n) {
        left = null;
        right = null;
        data = n;
        height = 0;
    }
}

AVL Tree Structure

public class AVLTree {
    private AVLNode root;
    public AVLTree() {
        root = null;
    }


    /**
     *
     * @param avlNode
     * @return
     */
    private int height(AVLNode avlNode) {
        return avlNode == null ? -1 : avlNode.height;
    }

    /**
     *
     * @param lHeight
     * @param rHeight
     * @return
     */
    private int max(int lHeight, int rHeight) {
        return lHeight > rHeight ? lHeight : rHeight;
    }

    /**
     *
     * @param data
     */
    public void insert(int data) {
            root = insert(data, root);
        }

        ……….
}

3. Time and Space Complexity

Time/Space Complexity	Average	Worst
Insert	O(log n)	O(log n)
Delete	O(log n)	O(log n)
Search	O(log n)	O(log n)
Space	O(n)	O(n)

Time and Space Complexity:

4. How to Balance an AVL Tree

Whenever we add a new node to the AVL tree or delete a node from it, it checks the balance factor of the node. In case of the balance factor is greater than 1 or less than -1, the tree will re-balance itself. There are 4 operations to balance an AVL tree:

Right Rotation.
Left Rotation.
Left-Right Rotation.
Right-Left Rotation

4.1. Right Rotation

We will first start with the right rotation; say we have a binary search tree with A as the root node and B is the left child of A and C is the left child of B. This means that A>B>C which is correct as per Binary search tree properties. For the right rotation, we need to rotate the A in such a way that A>B>C persists. After the right rotation, the new tree will have B as the root node and A is the left child of the B and C is the right child of B and we still have A>B>C

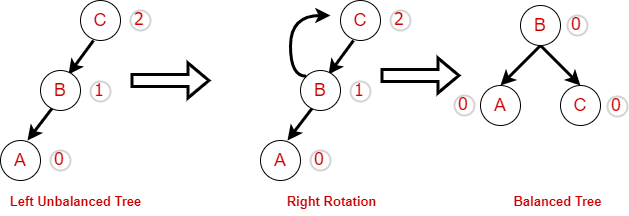
Here is the code snippet to perform the right rotation in an AVL tree.

private AVLNode rightRotation(AVLNode avlNode) {
    AVLNode node = avlNode.right;
    avlNode.right = node.left;
    node.left = avlNode;
    avlNode.height = max(height(avlNode.left), height(avlNode.right)) + 1;
    node.height = max(height(node.right), avlNode.height) + 1;
    return node;
}

4.2. Left Rotation

We will now see left rotation; say we have a binary search tree with A as the root node and B is the right child of A and C is the right child of B. This means that A<B<C which is correct as per BST properties. For the left rotation, we need to rotate the A in such a way that A<B<C persists. After the left rotation, the new tree will have B as the root node and node A is the left child of the B and C is the right child of B and we still have A<B<C.

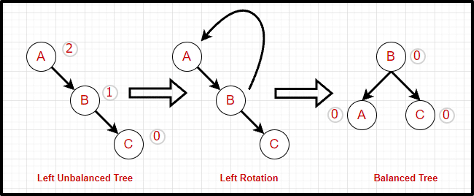
Left Rotation AVL Tree — **AVL Tree Left Rotation**

private AVLNode leftRotation(AVLNode avlNode) {
    AVLNode k1 = avlNode.left;
    avlNode.left = k1.right;
    k1.right = avlNode;
    avlNode.height = max(height(avlNode.left), height(avlNode.right)) + 1;
    k1.height = max(height(k1.left), avlNode.height) + 1;
    return k1;
}

4.3. Left-Right Rotation

Left-Right rotation or double rotation is an advance and complex version of single rotation like Left Rotation. In this rotation, we perform a left rotation followed by a right rotation.Let’s understand how to perform this with the following example:

State	Action
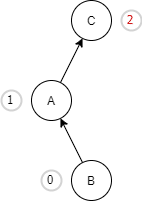	We have inserted a new node B into the right sub-tree of node A and it made node C an unbalanced node. To make this AVL tree balanced, we will need to perform the left-right rotation.
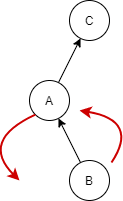	We will first perform the left rotation and that will make B the left sub-tree of node C and node A will become the left sub tree of node B.
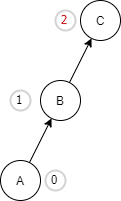	Because of the left sub tree of the left sub-tree, node C is still unbalanced.
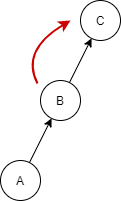	We will perform the right rotation of node B, which will become the root node. Node C will become the right sub-tree of node B whereas node A will become the left sub-tree of node B. This will make out AVL tree balanced.
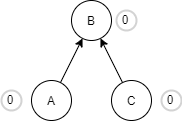	Now, our AVL tree is balanced.

Code Snippet for Left-Right Rotation

private AVLNode leftRightRotation(AVLNode avlNode) {
    avlNode.left = rightRotation(avlNode.left);
    return leftRotation(avlNode);
}

4.4. Right-Left Rotation

In the Right-Left Rotation, we perform a right rotation followed by a left rotation. Let’s understand how to perform this with the help of the following example.

State	Action
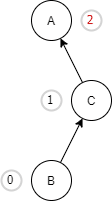	We have inserted a new node B into the left sub-tree of node C and it made the A an unbalanced node. To make this AVL tree balanced, we will need to perform the left-right rotation.
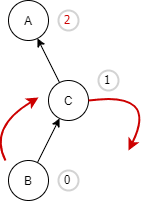	We will first perform the right rotation and that will make B the right sub-tree of node A and node C will become the right sub-tree of node B.
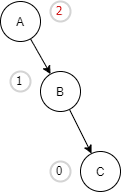	Because of the right sub-tree of the right sub-tree, node C is still unbalanced.
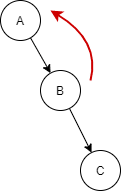	We will perform the left rotation of node B, which will become the root node. Node C will become the right sub-tree of node B whereas node A will become the left sub-tree of node B. This will make out AVL tree balanced.
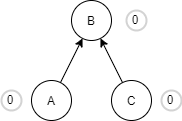	Now, our AVL tree is balanced.

private AVLNode rightLeftRotation(AVLNode avlNode) {
    avlNode.right = leftRotation(avlNode.right);
    return rightRotation(avlNode);
}

5. Insert a Node in AVL Tree

To insert a new node, we will find the proper position for it. So, we will start with the root node and compare its value with the root data. If it is greater, we will go right, or else we will go left. Once we find the parent node, we will add this new node as per its value.

After we do that, we will still have the BST however it might not be an AVL tree, so, we will check the balance factor, and based on its value (>1 or <-1), we will re-balance the BST to make it AVL Tree. The time complexity of the insert is a function of the height of the tree. For the balanced tree, the worst-case time complexity would be O(log(N)).

A duplicate key is not allowed in the AVL tree insertion

6. Delete a Node

Similar to what we have done to insert a node to an AVL tree, here also we will first search for the element to delete. Once we find that, we will delete the node. After we do that, we will still have the BST however it might not be an AVL tree, so, we will check the balance factor, and based on its value (>1 or <-1), we will re-balance the BST to make it AVL Tree.

The time complexity of the insert is a function of the height of the tree. For the balanced tree, the worst-case time complexity would be O(log(N)).

7. AVL Tree in Java

Finally, let’s see how to implement an AVL tree in Java.

package com.javadevjournal.ds.tree.avl;

//AVL Tree Node
class AVLNode {

    AVLNode left, right;
    int data;
    int height;

    public AVLNode() {
        left = null;
        right = null;
        data = 0;
        height = 0;
    }

    public AVLNode(int n) {
        left = null;
        right = null;
        data = n;
        height = 0;
    }
}


// AVL Tree Class
package com.javadevjournal.ds.tree.avl;

class AVLTree {
    private AVLNode root;
    public AVLTree() {
        root = null;
    }


    /**
     *
     * @param avlNode
     * @return
     */
    private int height(AVLNode avlNode) {
        return avlNode == null ? -1 : avlNode.height;
    }

    /**
     *
     * @param lHeight
     * @param rHeight
     * @return
     */
    private int max(int lHeight, int rHeight) {
        return lHeight > rHeight ? lHeight : rHeight;
    }

    /**
     *
     * @param data
     */
    public void insert(int data) {
        root = insert(data, root);
    }


    /**
     *
     * @param data
     * @param avlNode
     * @return
     */
    private AVLNode insert(int data, AVLNode avlNode) {
        if (avlNode == null)
            avlNode = new AVLNode(data);
        else if (data < avlNode.data) {
            avlNode.left = insert(data, avlNode.left);
            if (height(avlNode.left) - height(avlNode.right) == 2)
                if (data < avlNode.left.data)
                    avlNode = leftRotation(avlNode);
                else
                    avlNode = leftRightRotation(avlNode);
        } else if (data > avlNode.data) {
            avlNode.right = insert(data, avlNode.right);
            if (height(avlNode.right) - height(avlNode.left) == 2)
                if (data > avlNode.right.data)
                    avlNode = rightRotation(avlNode);
                else
                    avlNode = rightLeftRotation(avlNode);
        } else
        ; // Duplicate; do nothing
        avlNode.height = max(height(avlNode.left), height(avlNode.right)) + 1;
        return avlNode;
    }

    /**
     *
     * @param avlNode
     * @return
     */
    private AVLNode leftRotation(AVLNode avlNode) {
        AVLNode k1 = avlNode.left;
        avlNode.left = k1.right;
        k1.right = avlNode;
        avlNode.height = max(height(avlNode.left), height(avlNode.right)) + 1;
        k1.height = max(height(k1.left), avlNode.height) + 1;
        return k1;
    }


    /**
     *
     * @param avlNode
     * @return
     */
    private AVLNode rightRotation(AVLNode avlNode) {
        AVLNode node = avlNode.right;
        avlNode.right = node.left;
        node.left = avlNode;
        avlNode.height = max(height(avlNode.left), height(avlNode.right)) + 1;
        node.height = max(height(node.right), avlNode.height) + 1;
        return node;
    }
    /**
     * left-right rotation
     * @param avlNode
     * @return
     */
    private AVLNode leftRightRotation(AVLNode avlNode) {
        avlNode.left = rightRotation(avlNode.left);
        return leftRotation(avlNode);
    }

    /**
     * right-left rotation
     * @param avlNode
     * @return
     */
    private AVLNode rightLeftRotation(AVLNode avlNode) {
        avlNode.right = leftRotation(avlNode.right);
        return rightRotation(avlNode);
    }

    /**
     *
     * @return
     */
    public int countNodes() {
        return countNodes(root);
    }

    /**
     *
     * @param avlNode
     * @return
     */
    private int countNodes(AVLNode avlNode) {
        if (avlNode == null)
            return 0;
        else {
            int l = 1;
            l += countNodes(avlNode.left);
            l += countNodes(avlNode.right);
            return l;
        }
    }

    /**
     *
     * @param data
     * @return
     */
    public boolean search(int data) {
        return search(root, data);
    }

    /**
     *
     * @param avlNode
     * @param data
     * @return
     */
    private boolean search(AVLNode avlNode, int data) {
        boolean found = false;
        while ((avlNode != null) && !found) {
            int rval = avlNode.data;
            if (data < rval)
                avlNode = avlNode.left;
            else if (data > rval)
                avlNode = avlNode.right;
            else {
                found = true;
                break;
            }
            found = search(avlNode, data);
        }
        return found;
    }

    /**
     *
     */
    public void inorder() {
        inorder(root);
    }

    /**
     *
     * @param avlNode
     */
    private void inorder(AVLNode avlNode) {
        if (avlNode != null) {
            inorder(avlNode.left);
            System.out.print(avlNode.data + " ");
            inorder(avlNode.right);
        }
    }
}

// Helper class to run the AVL code
package com.javadevjournal.ds.tree.avl;

import java.util.Scanner;

public class AVLTreeHelper {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        AVLTree avlTree = new AVLTree();

        char ch;
        do {
            System.out.println("\nAVLTree Operations\n");
            System.out.println("1. insert ");
            System.out.println("2. search");
            System.out.println("3. count nodes");
            int choice = scanner.nextInt();
            switch (choice) {
                case 1:
                    System.out.println("Enter integer element to insert");
                    avlTree.insert(scanner.nextInt());
                    break;
                case 2:
                    System.out.println("Enter integer element to search");
                    System.out.println("Search result : " + avlTree.search(scanner.nextInt()));
                    break;
                case 3:
                    System.out.println("Nodes = " + avlTree.countNodes());
                    break;
                default:
                    System.out.println("Wrong Entry \n ");
                    break;
            }

            System.out.print("\nIn order : ");
            avlTree.inorder();

            System.out.println("\nDo you want to continue (Type y or n) \n");
            ch = scanner.next().charAt(0);
        } while (ch == 'Y' || ch == 'y');
    }
}

Summary

In this article, we have understood that what is an AVL tree, why is it so special. We have also learned the balance factor of the AVL tree. We have also seen all 4 types of supported rotations with examples. In the end, we have seen code for insert, delete, and re-balancing the AVL tree. Finally, we have seen the full code of an AVL tree. The source code for this article is available on our GitHub repository.