In this post, we will look at the binary tree data structure. We will see the different trees and their characteristics.
Introduction
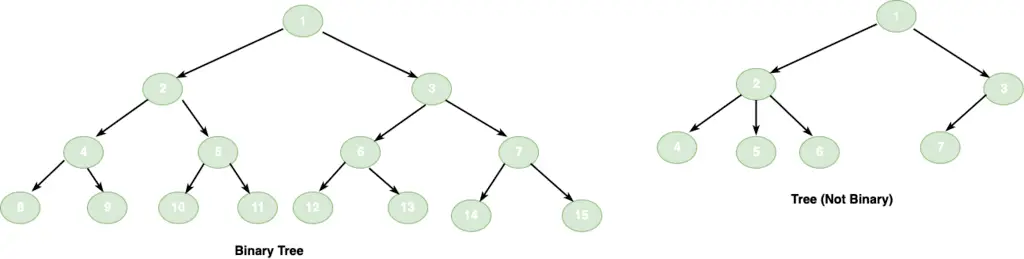
A binary tree data structure is a hierarchical data structure where each element have maximum 2 children. We call these children as left and right child. In the following example, the left side tree is a binary tree while the right one is not.
In the right tree structure, we have over 2 child nodes for the parent node 2. Let’s look at some points for the binary tree.
- Each node contains a pointer to the left and right sub-tree.
- Each node contains a data element.
If a tree has only 1 node, it’s also a binary tree.
Nodes in the example images are only labeled and they do not represent the number/data for the tree.
2. Binary Tree Terminologies
Before we get in details of the binary tree data structure, let’s refresh some common terminology.
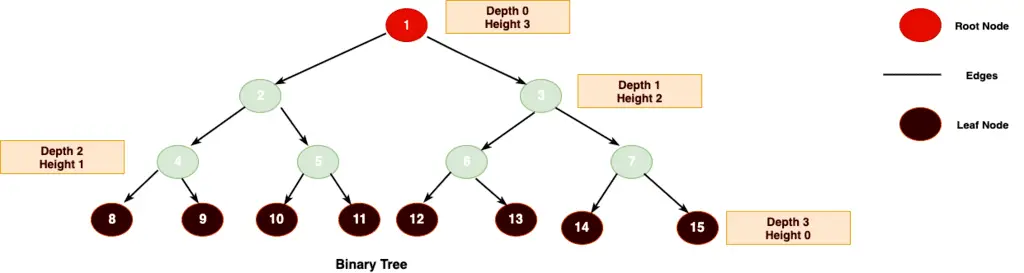
- Root node: – The topmost node is the root node (node 1 is the root node).
- We define a tree by parent and child nodes.
- Parent Node: Every node (excluding a root) in a tree is connected by a directed edge from exactly one other node. This node called as a parent.
- Leaf Nodes: Nodes which do not have any child nodes.
- Height: The height of a tree is the maximum number of edges from the node to the farthest leaf node.
- Depth: Number of edges from the root node to the node.
- Size: Size of a tree is the total number of nodes it contains.
If you are looking for the Binary search tree code Implementation. Please read Implementation binary search tree in Java.
3. Types of Binary Trees
Before we get in to other details, let’s discuss the different types of the tree. I will cover the most popular tree structures.
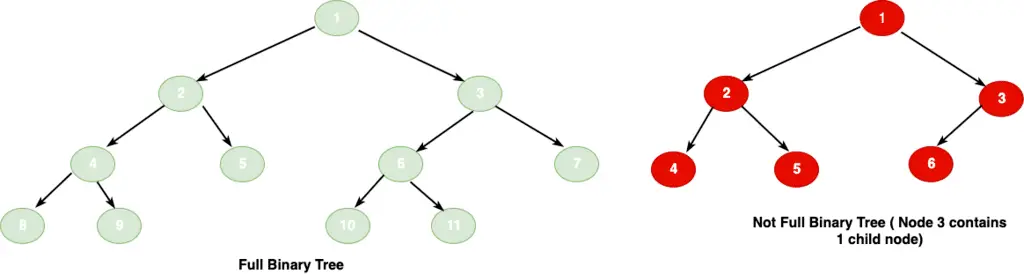
3.1 Full Binary Tree
A full binary tree is a tree with every node has either 0 or 2 children. No node will have only one child.
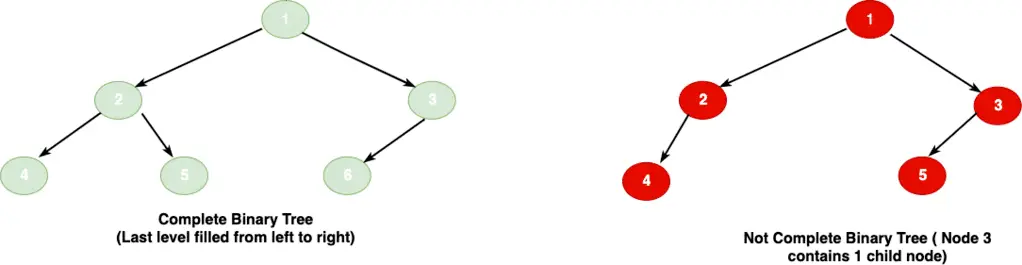
3.2 Complete Binary Tree
A tree where every level fully filled (have 2 children) except maybe the last level. For the complete binary tree, we fill the last level from left to right.
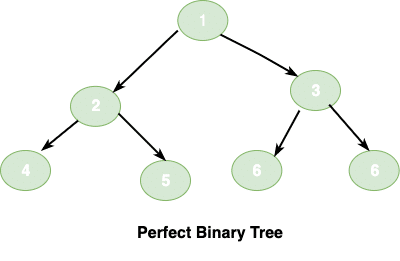
3.3 Perfect Binary Tree
A perfect binary tree is both complete and full.All the leaves have the same depth or same level.
A perfect tree is very rare.
4. Binary Tree Traversal
Tree traversal is the process to visit all nodes. On a high level, we can group the tree traversal in the following 2 groups.
- Depth-first traversal.
- Breadth-first traversal.
For the breadth-first traversal, we visit the nodes of the tree by levels from top to bottom and left to right. For the depth-first traversal; we have the following main traversal options (Also look at the following tree for the sample output)
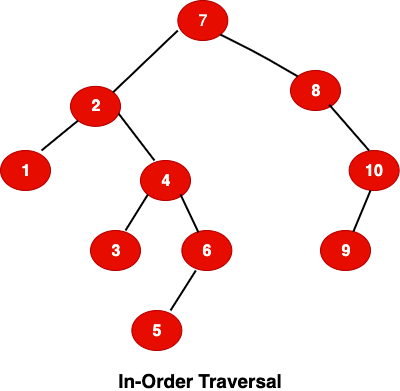
4.1 In-Order Traversal
For the In-Order traversal, we visit the left branch then current node and finally the right branch of our tree. If we perform the In-Order traversal on a binary search tree, we get the data in ascending orders. Here is the screen shot outlining the in-order traversal.
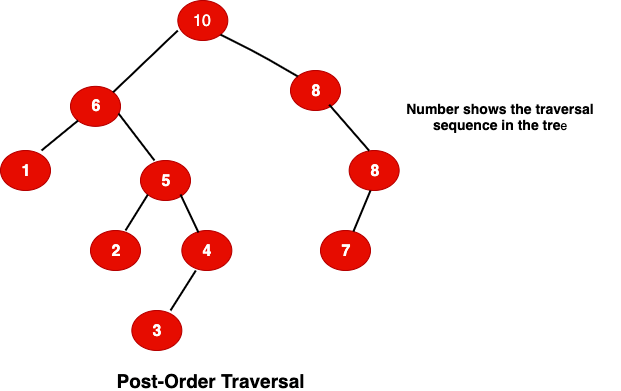
Number shows the traversal sequence in the tree.
Output: 9, 5, 1, 7, 2, 12, 8, 4, 3, 11
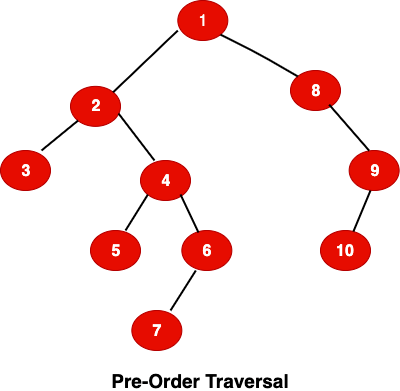
4.2 Pre-Order Traversal
In the pre-order tree traversal, we visit the current node then left tree and finally the right tree. Here is the screen shot outlining the in-order traversal.
Output: 8, 5, 9, 7, 1, 12, 2, 4, 11, 3
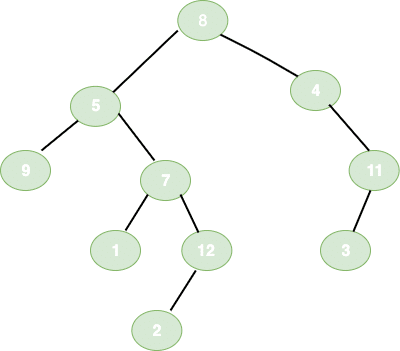
4.3 Post-Order Traversal
With post-order traversal, we visit the left tree then right tree and finally the parent. Let’s see how the traversal sequence looks like:
Output: 9, 1, 2, 12, 7, 5, 3, 11, 4, 8
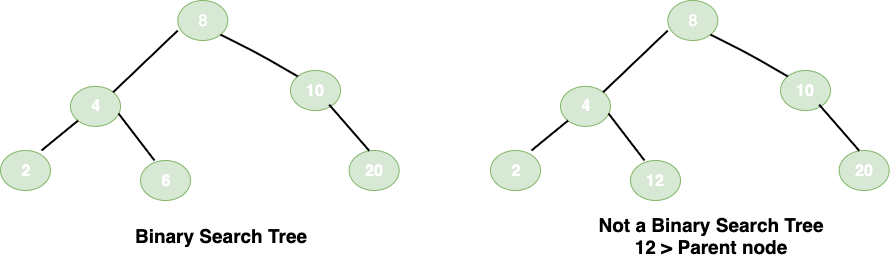
5. Binary Search Trees
A binary search tree is a specialized tree which fulfills the following properties:
- Each node contains certain data.
- The data in the left sub-tree is always less than the parent node.
- Data on the right sub-tree is always greater than parent node.
Some definition allows duplicates in the binary search tree while some don’t allow duplicate keys in BST. Both definitions are correct.
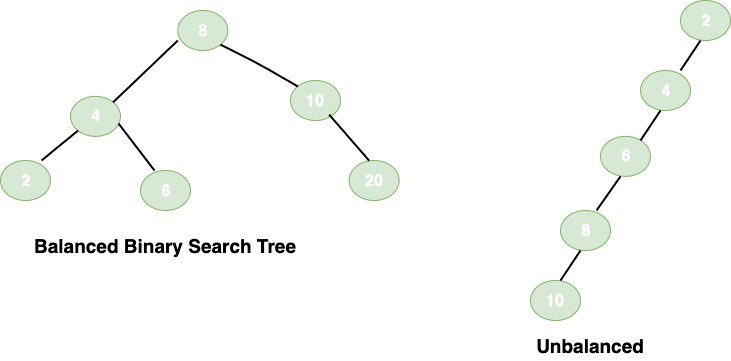
6. Balanced Vs Unbalanced Binary Tree
Two binary search trees can store the same values in different ways:
Balanced tree is a tree where
- The left and right sub-trees’ heights differ by at most one.
- The left sub-tree is balanced.
- The right sub-tree is balanced
7. Time Complexirty BST
| Average | Worst | |
| Space | ||
| Insert | ||
| Search | ||
| Delete |
8. BST Pros and Cons
Let’s cover some strengths and weaknesses of a BST:
- Efficient for insertion and deletion operations.
- As compared to sorted arrays, insertion and deletion are faster ( for BSTs, O(n) for arrays).
- We can do element insertion in sorted order in O(n).
- Binary search tree can lead to poor performance if we do not balance the tree.
- They do not have any O(1) for any operation.
Summary
In this post, we covered the binary tree and binary search tree data structure. We talked about various types of a tree and what are the different tree traversal techniques. At the end of the post we checked the binary search tree and its time complexities.