In this article, we are going to see the difference between Binary Tree and Binary Search Tree. We will also look at the basic operations and their time and space complexities.We will then see the real-life applications which use these two data structures.
1. What is a Binary Tree?
A Binary tree is a non-linear (memory is randomly allocated) Tree data structure and it is represented in a top-down way, where the top node is called as the Root. It is a collection of nodes and is a non-ordered data structure. Each node in a Binary Tree can have a maximum of two (0,1 or 2) children, called Left and Right child. The nodes having child nodes are called a Parent node and the nodes that don’t have any children are called Leaf node.Here are the 3 main properties:
- Data – the data in the node, any data type.
- Left Pointer – which points to Left Child.
- Right Pointer – which points Right Child.
Visual Representation
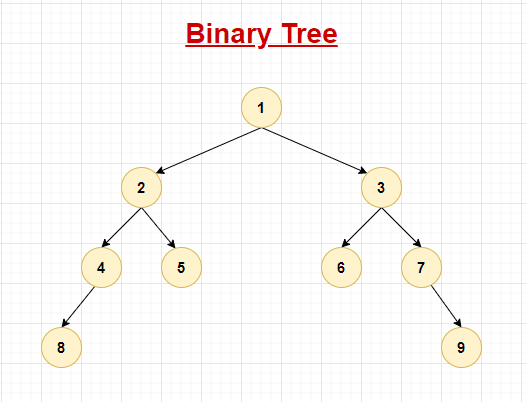
1.1. Operations on Binary Tree with Complexities:
- Search: Since the Binary Tree is unordered, to search an element we need to traverse all the nodes of the tree. The time complexity for the search would be O(n).
- Insert: Since the insert can also happen to the last node of the tree hence, we need to traverse all the nodes of the tree. So, the overall complexity will be O(n).
- Delete: Since deleting a node from a Binary Tree first requires to searching the node among all the nodes of the Binary Tree hence, the overall complexity will be O(n).
2. What is a Binary Search Tree
A Binary Search Tree (BST) is a special type of Binary Tree however unlike Binary Tree, the nodes in a Binary Search Tree are arranged in a pre-defined order. The structure remains however it is ordered. The following conditions must hold for a BST:
- The data of the left node should be less than the value of its parent node.
- The data of the right node should be greater than the value of its parent node.
- The left and right sub-tree are BST in themselves as well.
- Duplicate keys or values are not allowed.
Visual Representation
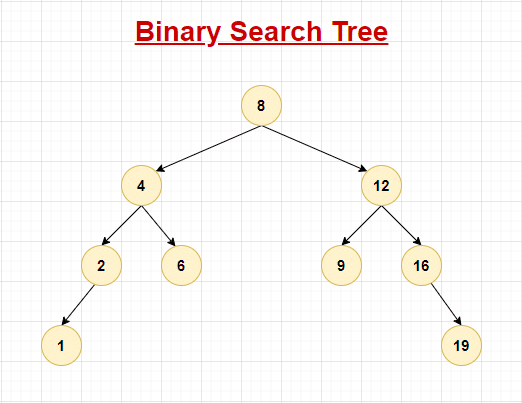
2.1. Operations on Binary Search Tree with Complexities:
The main concept behind the BST data structure is to optimize the search(lookup) operations. While searching for an element in the BST, we remove one half (left or right) at each step because of its properties. At every step, we will reduce the search space by n/2 (for a tree with n nodes) and will continue until an element is found.
- Search: As per the above description, to search an element in a Binary Search Tree generally takes
O(log n). In the case of a Skewed BST, the worst-case time complexity would beO(n). - Insert: For a Skewed tree, the worst-case time complexity would be
O(n)for inserting an element. - Delete: For a Skewed tree, the worst-case time complexity would be
O(n)for deleting an element.
3. Difference between Binary Tree and Binary Search Tree
here is a high level difference between Binary Tree and Binary Search Tree.
| Binary Tree | Binary Search Tree |
|---|---|
| Tree where each node has up to two leaves, it’s a data structure. | Binary search tree: Used for searching. It’s an algorithm for searching element. |
| It is a non-linear tree data structure where a node can have a maximum of 2 children. | It is ordered binary tree with each node can have a maximum of 2 children. |
| There is no ordering and any node can be added under any parent node. | In BST, the left child’s data will always have a value less than the parent’s data and the right child’s data will always have the value greater than the parent’s data |
| Nodes with duplicate values are allowed. | Nodes with duplicate values are not allowed. |
Time complexity is usually O(n) | Time complexity is usually O(log n) |
| Used to implement variations of Binary Tree like BST, Perfect Binary Tree, etc. | Used to implement variations of Balanced Binary Trees like AVL, Red-Black, etc. |
3.1. Similarities
Though there are lot of difference between Binary Tree and Binary Search Tree, however binary search tree is based on the binary tree data structure and there are many similarities between the two.
- Both are based on Tree data structure.
- Both can have a maximum of 2 child nodes.
- Both can hold different data types.
- Both have random memory allocated to them.
4. Applications of Binary Tree:
- Binary Search Tree
- Binary Tries – for storing router tables.
- Hash Trees – Used in torrents. It can also be used in blockchains like Bitcoin.
- Heaps – Used in implementing priority queues.
- Huffman Coding Tree – Used in compression algorithms.
- T-Reap – Used in wireless networking and memory allocation
- B+ Tree – used in some of the databases.
4.1. Applications of Binary Search Tree:
- In relational databases, BSTs can be used for indexing and multi-level indexing.
- There are various searching algorithms based on BST.
- It is useful in maintaining a sorted stream of data.
- TreeMap and TreeSet – uses BST internally.
- Huffman Coding Algorithm is based on BST.
- BST is used in UNIX kernels to managing a set of virtual memory areas (VMAs).
- Binary heaps – used to implement priority queues.
- Decision trees – used in machine learning for classification.
- B+ trees – used in database indexes
Summary
- In this article, we have learned what is a Binary Tree and what is a Binary search tree
- In this article, we have learned the operations of a Binary Tree and a Binary search tree
- In this article, we have learned the difference between Binary Tree and Binary search tree
- In this article, we have learned the similarities between a Binary Tree and a Binary search tree
- In this article, we have also learned the real-life applications of a Binary Tree and a Binary search tree