In this article of binary search tree, we will look at searching in a binary search tree. We have already seen how to add an element to Binary search tree and this will focus on the searching element in binary tree.
1. Searching in a Binary Search Tree
We will use some properties of the binary search tree to build an algorithm for searching in a binary search tree. If you remember from our previous lesson, the binary search tree carries the following properties.
- Element less than the node will be inserted on the left sub-tree.
- Element larger than the node will be inserted on the right sub-tree.
- Above properties are true of any sub-tree within a binary tree.
We will use the above properties to search node in BST. Here is the high-level algorithm to perform search in a binary search tree.
- Start from the root node.
- Compare the key with the root node key, if it is less than the root node key, we will go to the left sub-tree.
- Compare the key with the root node key. If it is greater than the root node key, we will go to the right sub-tree.
- We repeat step #2 and #3 until we find the element else false will be returned showing element is not found.
2. Visual Representation
We will implement the searching in binary search tree using Java but before that, it’s very important that we have a clear understanding of how the search work for BST.
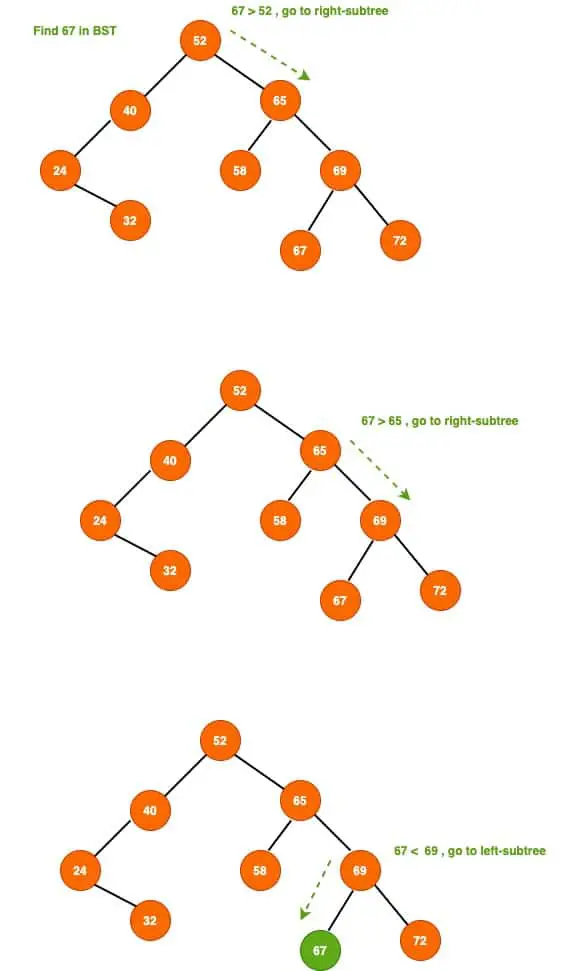
Look at the above picture, we are searching for 67 in the binary search tree. We started from the root and traversing to the left or right sub-tree by comparing the value with the node value.
We can implement by recursion or simple loop, in this post, we will implement searching in a binary search tree using recursion, but we can do same using a while loop.
3. Implementing Searching in BST using Java
Now we understand how algorithm for searching in a binary search tree, let’s see how to implement this in Java.
public class BinarySearchTree {
private Node root;
/**
* Our main insert method which takes the integer as input and will pass
* the parameter to internal insert method with the root node;
* @param data
* @return boolean status.
*/
public boolean insert(int data) {
root = insert(root, data);
return true;
}
private Node insert(Node node, int data) {
/**
* If Node is null, either tree is empty or this is the
* leaf node and we can create the node and return the new node.
*/
if (node == null) {
return new Node(data);
}
/**
* if data is less than the current element,
* let's go to the left side of the tree. We are giving a recursive call to the insert method
* and will wait until response is back.
*/
if (node.data > data) {
node.left = insert(node.left, data);
}
/**
* If data is greater than the current element,
* let's go the right side of the tree.We are giving a recursive call to the insert method
* and will wait until response is back. Other option is to use while loop.
*/
if (node.data < data) {
node.right = insert(node.right, data);
}
/**
* Element already exist is the tree. Please note there are multiple variations for this step.
* Few implementation do not allow duplicate element in BST (we are using same approach).
* while other allow duplicate in BST and they can go either to left or right of the tree.
*/
else {
return node;
}
return node;
}
// Delete the node from binary search tree
public boolean delete(int data) {
return delete(root, data) != null ? true : false;
}
public boolean search(int data) {
return search(data, root) != null ? true : false;
}
/**
* Internal method for searching element in the BST
* @param data
* @param root
* @return
*/
private Node search(int data, Node root) {
/*
This is the base case for coming out of recursion. We will return if
the node is null (not found) or if the node value is equal to the
search element (key found)
*/
if (root == null || root.data == data) {
return root;
}
/*
We will keep moving to the left sub-tree recursively if the key is
less than the node value.
*/
else if (data < root.data) {
return search(data, root.left);
}
/*
We will moving to the right sub-tree if the key is greater than the node value.
*/
return search(data, root.right);
}
/**
* Internal node class representing the node of the BST. This contains the following information
* <li>data- actual data stored in the Tree</li>
* <li>left - Left child of the node</li>
* <li>right - right child of the node</li>
*/
class Node {
int data;
Node left;
Node right;
Node(int data) {
this.data = data;
//this just for reading.they will be null by default
this.left = null;
this.right = null;
}
}
}Here is the main class for testing the code.
package com.javadevjournal.datastructure.tree;
import com.javadevjournal.datastructure.tree.bst.BinarySearchTree;
public class BinarySearchTreeTest {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
/* We are building a BST as below
52
/ \
15 56
/ \ / \
9 16 54 65
/ \ / \
3 10 61 72 */
bst.insert(52);
bst.insert(15);
bst.insert(56);
bst.insert(9);
bst.insert(16);
bst.insert(54);
bst.insert(3);
bst.insert(10);
bst.insert(65);
bst.insert(72);
bst.insert(61);
System.out.println("Search result:: " + bst.search(72));
System.out.println("Search result:: " + bst.search(200));
System.out.println("Search result:: " + bst.search(9));
System.out.println("Search result:: " + bst.search(567));
}
}
//<strong>output</strong>
Search result:: true
Search result:: false
Search result:: true
Search result:: false4. Binary Search Tree Time and Space Complexity
The worst case time complexity for searching in a binary search tree is O(n). This can happen when we have an unbalanced binary search tree. For worst case, we start from the root node and may end up traversing the tree until the farthest leaf node.
| Worst Case | Best Case | Avg Case |
O(n) | O(log(n)) | O(Log(n)) |
The space complexity for binary search tree is O(n). We can achieve the O(log(n)) time complexity with the help of a balanced binary tree.
Summary
In this article, we saw how to implement search in a BST. Search is important when we work on deleting a node in a binary search tree, as deletion involves searching and deleting. As always, the source code for this article is available on our GitHub repository.