In this series of binary search tree, we will learn steps for deleting node from binary search tree. We will also see how to delete node from binary search tree in Java.Deleting node from binary search tree is more complicated than other operations on BST.
Deleting Node from Binary Search Tree
Deleting from binary search tree is more complicated, if you look closely, node deletion in binary search tree can be defined as a combination of 2 steps.
- Search for the node to be removed.
- Delete the node if found.
2. Binary Tree Node Deletion Algorithm
Before we implement the binary tree node deletion in Java, it’s very important that we understand the deletion logic and what are the different possible cases while deleting node from BST. When deleting node, there are 3 possible cases.
- Node is a leaf node (no children). This is the most simple case.
- Node contains only one child (either left or right).
- Node contains both left and right child (most complicated step)
Let’s see all these cases for better understanding.
2.1 Leaf Node Removal
As said earlier, this is the most simplest use case.If the node is a leaf node, we have to simply set the reference in the parent as NULL. Let’s see the following example to understand it clearly.In this example, we are deleting 32 from the binary search tree and 32 is the leaf node
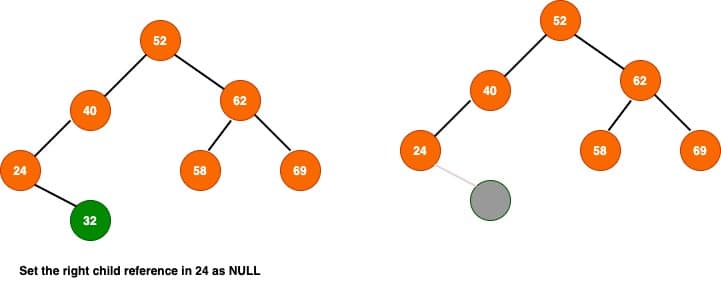
2.2. Node Contains only One Child
In this case, we simply adjust the link between the node’s child (node being deleted) and it’s parent.This is a simple link manipulation. Let’s see how to delete the 40 from out tree (40 contains only 1 child ).
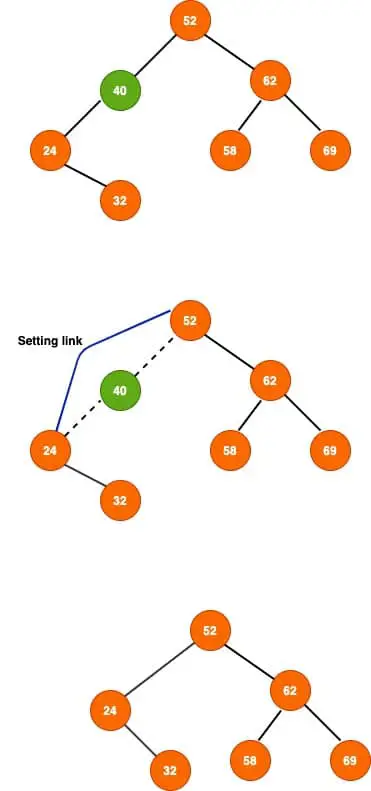
2.3. Deleting Node with Both Left and Right Child
This is the most complicated use case while deleting node from binary search tree. There are 2 ways to do this, I am going to cover only one method but both are similar in terms of logic.Here are the 2 method to accomplish this and we will be using the #2.
- Choose the largest element from left sub-tree.
- Choose the minimum element from right sub-tree.
Remember, same set of values can be used to represent a different binary search tree. Can you represent the above BST differently??
Let’s see how to remove element with two child using above property
- Search for the element to deleted.
- Find the minimum value in the right sub-tree (how we can find that? )
- Replace value of the node which we need to remove with the minimum element found in #2. (remember, we are not deleting the node but only changing the node value)
- Delete the minimum element value node from the tree.
Minimum element node on the eight sub-tree will have no left children.If it contains any left child, it will not be minimum element in the right tree. This is another interesting property of BST.Let’s see we need to delete 62 from our tree
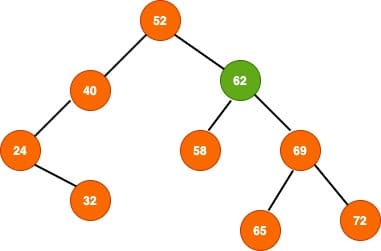
Find minimum element in the right sub-tree. In our case it is 65.
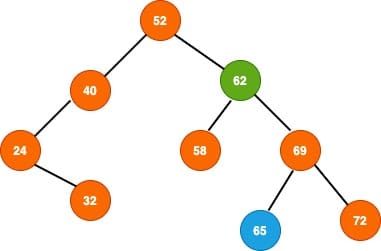
Replace the value of the node to be removed with the minimum value found in the right sub-tree and finally remove the minimum element node from the tree.
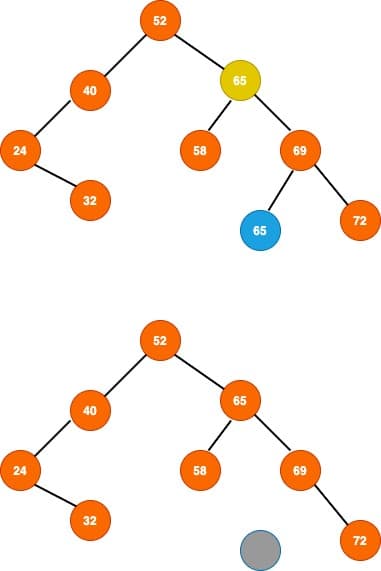
You can use same logic to delete the node using largest element from left sub-tree. How can you find the largest element in the left sub-tree?
3. Deleting Node from Binary Tree Using Java
We have understood the different use case, let’s see how to implement the logic of deleting the node from binary search tree using Java.I have added the sufficient comments where required or need more clarity.
package com.javadevjournal.datastructure.tree.bst;
public class BinarySearchTree {
private Node root;
/**
* Our main insert method which takes the integer as input and will pass
* the parameter to internal insert method with the root node;
* @param data
* @return boolean status.
*/
public boolean insert(int data) {
root = insert(root, data);
return true;
}
private Node insert(Node node, int data) {
/**
* If Node is null, either tree is empty or this is the
* leaf node and we can create the node and return the new node.
*/
if (node == null) {
return new Node(data);
}
/**
* if data is less than the current element,
* let's go to the left side of the tree. We are giving a recursive call to the insert method
* and will wait until response is back.
*/
if (node.data > data) {
node.left = insert(node.left, data);
}
/**
* If data is greater than the current element,
* let's go the right side of the tree.We are giving a recursive call to the insert method
* and will wait until response is back. Other option is to use while loop.
*/
if (node.data < data) {
node.right = insert(node.right, data);
}
/**
* Element already exist is the tree. Please note there are multiple variations for this step.
* Few implementation do not allow duplicate element in BST (we are using same approach).
* while other allow duplicate in BST and they can go either to left or right of the tree.
*/
else{
return node;
}
return node;
}
/**
* In order BST traversal allows to traverse tree in the sorted order.
* This traversal follow left->current-right pattern.
* <li>left sub-tree will be viisted first.</li>
* <li> Current node will be viisted after left traversal</li>
* <li>Right subtree will be visited in the end.</li>
*/
public void inOrderTraversal(){
inOrderTraversal(root);
}
/*
Internal private method to do in order traversal.We will pass the
root node to start with and will visit the tree recursively using the following
path left-current-right
*/
public void inOrderTraversal(Node node){
//We will continue until null or empty node is found
if(node!=null){
//visit the left subtree until the leaf node
inOrderTraversal(node.left);
//Print the node
System.out.println(node.data);
//process the same step for the right node
inOrderTraversal(node.right);
}
}
// Delete the node from binary search tree
public boolean delete(int data){
return delete(root, data)!=null? true: false;
}
private Node delete(Node root, int data){
//this is the termination condition for our recursion call
if(root ==null){
return root;
}
//we will keep traversing the left subtree until the element is less than node data.
else if(root.data>data){
root.left = delete(root.left, data);
}
//we will keep traversing the right subtree until the element is greater than node data.
else if(root.data< data){
root.right = delete(root.right, data);
}
else{
/*we have found a potential match, mow we need to check
the 3 different cases to see which one should be executed.*/
// we are dealing with situation, where we have either one child or no child
if(root.left ==null){
return root.right;
}
else if(root.right == null){
return root.left;
}
/*this is the complex use case where element contains both left and right sub-tree
We will go with our algorithm to find the minimum element in the right sub-tree and
replace it followed by deletion
*/
root.data = findMin(root.right);
root.right= delete(root.right, root.data);
}
return root;
}
private int findMin(Node node){
//we are assuming that it's the minimum value
int min = node.data;
//remember left sub-tree will have the minimum value.You can also use the same logic to implement BST without recursion.
while(node.left!=null){
min = node.left.data;
node = node.left;
}
return min;
}
/**
* Internal node class representing the node of the BST. This contains the following information
* <li>data- actual data stored in the Tree</li>
* <li>left - Left child of the node</li>
* <li>right - right child of the node</li>
*/
class Node {
int data;
Node left;
Node right;
Node(int data) {
this.data = data;
//this just for reading.they will be null by default
this.left = null;
this.right = null;
}
}
}Here is the main method to test our code.
package com.javadevjournal.datastructure.tree;
import com.javadevjournal.datastructure.tree.bst.BinarySearchTree;
public class BinarySearchTreeTest {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
/* We are building a BST as below
52
/ \
15 56
/ \ / \
9 16 54 65
/ \ / \
3 10 61 72 */
bst.insert(52);
bst.insert(15);
bst.insert(56);
bst.insert(9);
bst.insert(16);
bst.insert(54);
bst.insert(3);
bst.insert(10);
bst.insert(65);
bst.insert(72);
bst.insert(61);
System.out.println("********Before Deletion *********");
bst.inOrderTraversal();
//delete 56
bst.delete(56);
System.out.println("********After Deletion *********");
bst.inOrderTraversal();
}
}
//<strong>output</strong>
********Before Deletion *********
3
9
10
15
16
52
54
56
61
65
72
********After Deletion *********
3
9
10
15
16
52
54
61
65
724. Time Complexity
The worst case time complexity for deleting node from binary search tree is O(n). In Worst case, it will be the unbalanced or skewed tree and we have to travel from root node to the farthest leaf node.
We can optimize the above algorithm by avoiding the recursive call.This can be done by keeping trek of the parent node of the successor.
Summary
In this article, we talk about deleting node from binary search tree. We saw what are the three different use cases while deleting node from the binary tree. At the end of this article, we also saw how to implement binary tree node deletion using Java. As Always the source code for this article is available on the GitHub.